深度学习基础-神经网络

前言

本文将从单层感知机开始逐步深入到多层感知机，解释激活函数的出现和特性，解释损失函数的出现，解释模型的最终收敛，解释参数的初始化准则，并有后向传播的公式推导。

神经元

神经元通过突触将神经递质传递至后一个神经元的树突，多个树突接收的信号共同形成细胞整体的电信号并达到兴奋临界点时，激发电信号。这就是神经元简化后的工作流程。

下图是神经元的电路模型：

感知机

弗兰克·罗森布拉特在1957年就职于康奈尔航空实验室（Cornell Aeronautical Laboratory）时将神经元抽象成感知机（也称为前馈神经网络），感知机有n个输入，一个输出（0或1），结构如下图

$\displaystyle f(x) = \sum_{i=1}^n \omega_i x_i+b\ \ \qquad \qquad output = \begin{cases} 1 & if\ f(x)>0 \\ 0 & else \end{cases} $

输出$output$是$sgn(f(x)) $，符号函数，模拟神经元的激活，我们称之为激活函数。这也是感知机与线性回归（没有激活函数）和逻辑回归（激活函数为sigmoid函数）的区别所在。

注：sgn函数是最早的激活函数，现在基本不用了。

感知机是一个最简单的二元分类器，也是一个单层的神经网络。

下面我们假设$b=0$，$b\neq0$时让$\omega,x$维数多一维，$\omega_{n+1}=b \quad x_{n+1}=1$即可

假设我们有m对数据$D_m = \{(x_1, y_1),\cdots,(x_m, y_m)\}$，$x$为n维向量，y是x向量的标签（实际模型的输出，正确结果）。

注：输入数据都有标签的这种模式称为监督学习，当输入数据没有标签称为无监督学习，当输入数据只有部分有标签称为半监督学习。当前大部分模型都是监督学习。

感知机通过对$D_m$多次迭代确定$\omega_i (i=1,\cdots,n)$的最终值：对于$D_m$中的每对$(x,y)$，$\omega_j := \omega_j + \alpha (y-f(x))x(j) \qquad j=1,\cdots,n$

注意：仅当针对给定训练数据$(x,y)$产生的输出值$f(x)$与预期的输出值$y$不同时，权重向量$\omega$才会发生改变。人类的学习也正是由于这种非预期结果。

至此，训练好（参数确定好）的感知机就可以用于分类了。

但是，只有在$D_m$是线性分隔时，才可以在有限次迭代后收敛（$\omega_j$趋于特定值）。

如果存在一个正的常数$\gamma$和权重向量$\omega$，对所有的$i$满足$y_i \cdot(\omega\cdot x_i+b)>\gamma$，训练集$D_m$就被叫被做线性分隔的。同时，假设$\displaystyle R=\max_{1\leq i \leq m}\|x_i\|$ ，则错误次数$k \leq (\frac{R}{\gamma})^2$

所以，这种单层的感知机只能做简单的线性分类任务（异或都无法实现）。而如果将计算层增加到两层，计算量则过大（1970年左右），而且没有有效的学习算法。其实，1974年哈佛大学的Paul Werbos就证明了增加一个网络层，利用反向传播算法可以搞定XOR问题，但却未得到重视。

多层感知机

1986年，Rumelhar和Hinton（深度学习鼻祖）等人提出了反向传播（Backpropagation，BP）算法，解决了两层神经网络所需要的复杂计算量问题，并广泛应用于升级网络的训练中。

下图是一个简单的3输入，2输出的双层感知机（前馈神经网络），中间为4个节点的隐藏层。

一般来说，输入节点数量和输出节点数量都是确定的，隐藏层节点数量需要自己设计（关键点）。

StackOverflow上有一个经验公式：$N_h = \frac{N_s}{\alpha (N_i+N_o)}$，$N_s$为训练集样本数，$\alpha$一般取2~10，$N_i$为输入层节点数，$N_o$为输出层节点数，在此经验公式上再试验调整即可。

$a(\cdot)$为激活函数，如单层感知机的sgn函数，但在多层感知机中，由于涉及到梯度的计算，一般用Sigmoid、ReLU、tanh等激活函数。

说明：$w^{(1)}$指第一层权重，$w_1^{(1)}$指$x_1$ 对应的第一层权重，$w_1^{(1)}[1]$指$x_1$对应的第一层的权重的第一个值。

$h_1 = a(\sum_{i=1}^3 w^{(1)}_i[1] x_i) \quad$ $h_2 = a(\sum_{i=1}^3 w^{(1)}_i[2]x_i) \quad$ $h_3 = a(\sum_{i=1}^3 w^{(1)}_i[3]x_i) \quad$ $h_4 = a(\sum_{i=1}^3 w^{(1)}_i[4]x_i)$

$z_1 = \sum_{j=1}^4 w^{(2)}_j[1] h_j \qquad$ $ z_2=\sum_{j=1}^4 w^{(2)}_j[2]h_j$

$ y_1 = a(z_1)=f(x)[1] \qquad $ $y_2 = a(z_2)=f(x)[2]$

其中，$f(x)=(a(z_1),a(z_2))$，后面为索引。

对于偏置节点，只需让$x_4=1,w^{(1)}_5=b^{(1)} \quad$ $ h_5=1,w^{(2)}_3=b^{(2)}$ ，故先不考虑。

当中间隐藏层的神经元数量趋于无穷多时，多层感知机可以拟合任何非线性函数（由于激活函数的存在，若没有激活函数，多层线性层也只相当于一层线性层），可见中文版证明过程或直观理解，因此可以解决非线性分类任务。

后向传播BP算法

训练模型的目的是去拟合实际情况，即让训练模型参数$w$和实际模型的参数一致，因为只能获取真实情况的标签，一个朴素的想法就是让模型的输出与实际接近，那参数分布基本就与实际相似了。

那么如何衡量这个误差呢？于是定义了一个指标去衡量误差——损失函数(Loss-Function)，那么我们的目的就是让所有样本的损失函数最小。

注：常见的损失函数有绝对值损失、均方损失、Huber损失、交叉熵损失函数。实际评判的标准还是在另一批数据（测试集）的表现，损失函数只能判断是否收敛。

我们称之为期望(expected)风险：所有样本的平均误差$ R_{exp}(f)=E_p[L(Y,f(X))]$，$Y$为标签集合，$X$为样本集合，$L$为损失函数，为全局最优。

进一步的，$\displaystyle R_{exp}(f)= \int_{X\times Y } L(y,f(x))P(x,y)dxdy \quad$ $ P(x,y)$为真实分布

但是我们手中只有部分的数据（训练数据），不可能获取到所有的数据，更不用说真实分布$P(X,Y)$我们都无从得知，于是我们用我们训练集的数据去估计整体的误差。

我们称之为经验(empirical)风险：训练集上的平均误差$ R_{emp}(f)=\frac{1}{N}\sum^N_{i=1}L(y_i,f(x_i))$，为局部最优。当数据量足够大时，经验风险就趋于期望风险。

---

注：还有结构(structural)风险：

为了让权值不会过大(参数稀疏化)并减轻过拟合程度（让参数变为0或接近0，边界较为平滑），加上正则项（也叫权重衰减项weight decay term、惩罚项）

奥卡姆剃刀原则：如无必要，勿增实体。

$ R_{str}(f)=\frac{1}{N}\sum^N_{i=1}L(y_i,f(x_i))+\lambda J(f)$，$\lambda$称为惩罚因子或weight decay parameter

---

所以，我们现在的问题是如何使损失函数$L$最小，这正是一个最优化问题，我们很容易想到令损失函数对参数的偏导为0，再从这些点中找出最优点。但是，第一、对于非凸函数，偏导为0并不等价于极值；第二、偏导为0的点可能有无穷多个，无法找出最优点；第三、求解偏导为0即对求解一个非线性方程组（激活函数的存在），可能根本求不出解析解（直接求解需要求矩阵的逆，并非所有矩阵都可逆），而且计算量较大。

所以我们只能去求数值解。一个普遍的算法（或者遗传算法，也有用HJB方程更新参数的）是使用梯度下降(GD)算法：即对训练集$D_m$中所有的样本（m组数据）迭代

$\displaystyle w_j^1[t]=w_j^1[t] - \eta_1\frac{1}{m} \sum_{i=1}^m \frac{\partial L(y_i^*,f(x_i))}{\partial w_j^1[t]} \quad t=1,2,3,4$

$\displaystyle w_j^{(2)}[t]=w_j^{(2)}[t] - \eta_2\frac{1}{m} \sum_{i=1}^m \frac{\partial L(y_i^*,f(x_i))}{\partial w_j^{(2)}[t]} \quad t=1,2$

（$y^*$为真实标签向量，$w$和$x_i$为向量，但$w[t]$为标量，$\eta_1 \ \eta_2$ 为步长，也称为学习率，）直至收敛。因为梯度的反方向是下降最快的方向即收敛最快的方向。

学习率不宜过大（导致模型不能收敛或在最优点徘徊）或过小（收敛很慢、更容易进入局部最优点（局部极小值点）或鞍点，更多的是鞍点，可见[论文](1605.07110] Deep Learning without Poor Local Minima (arxiv.org)](https://arxiv.org/abs/1605.07110)），通常取值为0.01-0.001，一般来说每一层的学习率都是一样的，但是可以根据自己需求去设置每一层的学习率，学习率随训练轮数的增加可以适当降低。

注：鞍点的Hessian矩阵不定，特征值有正有负；极小值点的Hessian矩阵正定，特征值都为正。

有论文说明：

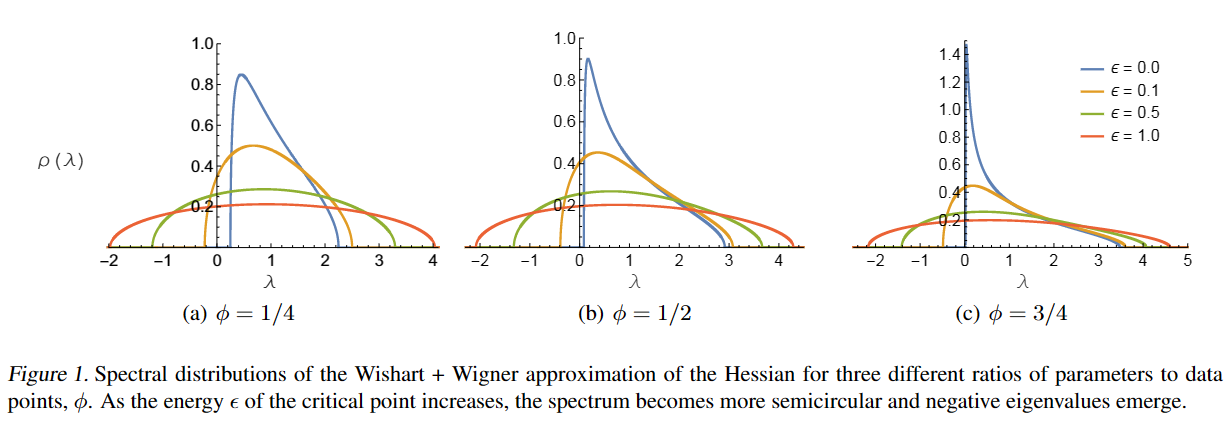
$\phi$为参数与数据量的比值，$\epsilon$为损失值Loss

• 当Loss很大的时候，特征值分布有正有负，表明鞍点是困扰优化的主要原因
• 当Loss很小的时候，鞍点逐渐消失，主要是局部极小值点。

大多数情况下，局部最优和全局最优几乎一样好，局部最优已经能满足我们的需要，所以重点是去避免陷入鞍点和泛化不好的局部最优点。而下文的SGD可以逃离鞍点和泛化不好的局部最优点（主要是sharp minima），更倾向于收敛到flat minima。

---

那么，我们的重点便是计算$\frac{\partial L}{\partial w}$，以上面的多层感知机为例子：

假设其损失函数为均方损失$\displaystyle L(y^*,y)=\frac{1}{k} \sum_{i=1}^k(y_i-y^*_i)^2 \quad$ ，本例中输出节点数量$k=2$

又由上文可知$\displaystyle y_i = a(z_i) \ = a(\sum_{j=1}^4 w^{(2)}_j[i] h_j)=a(\sum_{j=1}^4 w^{(2)}_j[i] a(\sum_{n=1}^3w_n^{(1)}[j]x_n))$

所以，对第二层的梯度计算如下（根据链式法则）：

$\displaystyle \frac{\partial L(y^*,y)}{\partial w^{(2)}_l[t]}=\frac{2}{k}\cdot (y_t-y^*_t) \frac{\partial y_t}{\partial w^{(2)}_l[t]}=\frac{2}{k}\cdot (y_t-y^*_t)\cdot \frac{\partial a(z_t)}{\partial z_t} \cdot \frac{\partial z_t}{\partial w^{(2)}_l[t]}=\frac{2}{k}\cdot (y_t-y^*_t)\cdot \frac{\partial a(z_t)}{\partial z_t} \cdot h_l$

其中，$\frac{\partial a(\cdot)}{\partial \cdot}=a'(\cdot)\quad k=2 \qquad l=1,2,3,4 \quad t=1,2$

选择其他损失函数时，$2(y_t-y^*_t)$换成$\displaystyle \frac{\partial L(y,y^*)}{\partial y_t}$即可

对第一层的梯度计算较为复杂，直接计算如下：

$\displaystyle \frac{\partial L(y^*,y)}{\partial w^{(1)}_l[t]}=\frac{2}{k}\cdot \sum_{i=1}^2 (y_i-y^*_i)\cdot\frac{\partial y_i}{\partial w^{(1)}_l[t]}$

$\displaystyle=\frac{2}{k}\cdot \sum_{i=1}^2 (y_i-y^*_i)\cdot\frac{\partial a(z_i)}{\partial z_i}\frac{\partial z_i}{\partial w^{(1)}_l[t]}$

$=\displaystyle \frac{2}{k}\cdot [(y_1-y^*_1)\cdot\frac{\partial a(z_1)}{\partial z_1}\cdot w^{(2)}_t[1]\cdot \frac{\partial h_t}{\partial w^{(1)}_l[t]}+(y_2-y^*_2)\cdot\frac{\partial a(z_2)}{\partial z_2}\cdot w_t^{(2)}[2]\cdot \frac{\partial h_t}{\partial w^{(1)}_l[t]}]$

$=\displaystyle \frac{2}{k}\cdot[(y_1-y^*_1)\cdot\frac{\partial a(z_1)}{\partial z_1}\cdot w^{(2)}_t[1] +(y_2-y^*_2)\cdot\frac{\partial a(z_2)}{\partial z_2}\cdot w_t^{(2)}[2]]\frac{\partial a(\sum_{i=1}^3 w^{(1)}_i[t] x_i)}{\partial w^{(1)}_l[t]}$

$=\displaystyle \frac{2}{k}\cdot[(y_1-y^*_1)\cdot\frac{\partial a(z_1)}{\partial z_1}\cdot w^{(2)}_t[1] +(y_2-y^*_2)\cdot\frac{\partial a(z_2)}{\partial z_2}\cdot w_t^{(2)}[2]]\cdot \frac{\partial a(\sum_{i=1}^3 w^{(1)}_i[t] x_i)}{\partial \sum_{i=1}^3 w^{(1)}_i[t] x_i}\cdot x_l $

其中$l=1,2,3 \quad t=1,2,3,4$

但是我们可以借助第二层的梯度计算结果，简化为：

$\displaystyle \frac{\partial L(y^*,y)}{\partial w^{(1)}_l[t]}=[\frac{\partial L(y^*,y)}{\partial w_l^{(2)}[1]}\cdot \frac{w_t^{(2)}[1]}{h_l}+\frac{\partial L(y^*,y)}{\partial w_l^{(2)}[2]}\cdot \frac{w_t^{(2)}[2]}{h_l}]\cdot \frac{\partial a(\sum_{i=1}^3 w^{(1)}_i[t] x_i)}{\partial \sum_{i=1}^3 w^{(1)}_i[t] x_i}\cdot x_l $

将训练集中每个样本的梯度计算出来后便更新一次参数，如此迭代直至收敛。

这可以保证向（局部）最优点移动，但是当数据量较大时，一次迭代较慢，训练过程很慢，占用内存较大，而且进行了很多冗余的计算。其他的做法有随机梯度下降、批量梯度下降。

随机梯度下降Stochastic Gradient Descent：每次从训练集随机选一个样本去更新参数，参数更新速度大大提高，降低了计算开销，而且有可能收敛到更好的局部最优点，但是这相当于对梯度的噪声估计，参数的变化较为振荡，甚至有可能不收敛。但有研究显示当我们慢慢的降低学习率时，SGD 拥有和 GD 一样的收敛性能，对于非凸和凸曲面几乎同样能够达到局部或者全局最优点。所以基本没人用GD。

批量梯度下降Mini-Batch Gradient Descent：每次从训练集选择k个样本去更新参数，$1<k<m$，是对GD和SGD的折中，结合了二者的优点，也是实际中常用的。通常我们称$k$为一个mini batch，每一轮迭代更新称为一个iteration，取完所有样本称为一个epoch。

---

激活函数

接下来就是激活函数$a(\cdot)$的选择，由上式计算可以看出激活函数的梯度不能为0，否则无法更新参数，这就是sgn函数不适用多层感知机的原因。此外，前向传播的过程中，每一层的输出都要经过激活函数，我们希望激活函数能将输出值限制在一个范围内，这样对于一些较大的输入，模型也能保持稳定，但是这会限制模型的表达能力，故这需要根据自己的需求判断。

以下是激活函数应该具有的特征：

• 激活函数应该为神经网络引入非线性，即不是y=ax+b这种
• 避免梯度弥散（即梯度接近或等于0）或梯度爆炸（梯度大于或远大于1）的特性，造成网络更新过慢，由梯度计算式可以看到第一层的梯度有每一层激活函数导数的连乘，若是层数加深，不合理的激活函数会使梯度容易出现0值或$\infty$值
• 输出最好关于0对称，否则这一层输出都为正数或负数，导致下一层的参数更新都是增加或减少（称为zig zag path），不利于参数更新
• 激活函数应该是可微的，使得满足各层之间梯度下降的计算(至少部分可微)
• 梯度的计算不应该太复杂，影响网络性能

下图是三种常用的激活函数，其他函数可见维基百科

---

参数初始化

通过梯度的计算式，我们不难发现参数的更新与其初始值有关，其收敛速度跟初始值有很大关系，若初始值都一样，那么参数的更新也会一样，整个网络的参数都会一样，这显然不符合我们的预期，所以，参数的初始化必须是随机的，不宜过大也不宜过小，否则会出现梯度消失或梯度爆炸，故我们需要控制初值的方差，最好保证输入输出的方差一致，而且其均值应为0（全为正或全为负会出现上文的zig zag path现象）。一个好的参数初始化虽然不能完全解决梯度消失或梯度爆炸的问题（BatchNorm解决了），但是对于处理这两个问题是有很大帮助的，并且十分有利于提升模型的收敛速度和性能表现。

下图是一些初始化的方法，一个直观的解释可见从几何视角来理解模型参数的初始化，对于tanh和Sigmoid这种饱和激活函数，Xavier初始化较为常用；对于ReLU及其变种等非饱和激活函数，He初始化较为常用。

注：

1. x 趋于正无穷时，激活函数的导数趋于 0，则我们称之为右饱和；
2. x 趋于负无穷时，激活函数的导数趋于 0，则我们称之为左饱和；
3. 当一个函数既满足右饱和又满足左饱和时，我们称之为饱和激活函数。

$fan\_in$是指这层的输入节点数量，$fan\_out$是这层的输出节点数量。